Week 4 - Modeling Biological Systems

A model is a simplified or idealized representation or description of a particular system/process. Usually, this is in mathematical terms. They should be able to address the given questions of interest.

Thus, they are simplified representations of reality, to help us comprehend the more complex features one at a time. We can use them to study:

chemical reaction dynamics
growth of populations
the spread of epidemics

The Population Bomb

In 1968, Dr. Paul Ehrlich published "The Population Bomb", predicting overpopulation. He claimed that millions would die of starvation within 15 years.

But his predictions were too pessimistic, and currently scientists debate what our planet can support in terms of our population.

The issue with his predictions were that they didn't account for the Green Revolution that came over time. The other thing is that, as conditions improve, children per family lower as well. Usually poorer conditions creates higher birth rates so that there's a hope some of the offspring survive. There may even be the other issue, where we stop having a growth rate and even start losing numbers of people!

Population Modelling Basics

Start with modeling a bacteria in a petri dish. If a species of bacteria can reproduce, on average, once every two hours, we can describe their growth rate $k$ :

k = 0.5 bacterium per hour

Using this growth rate, we write the simple equation for unlimited growth of a population of bacteria $x$ over time $t$ :

\frac{d x}{d t} = k x

This only accounts for reproduction. To account for deaths, we consider the maximum number that the environment can hold, represented by $x_{m a x}$ :

\frac{d x}{d t} = k x (1 - \frac{x}{x_{m a x}})

Here $x_{m a x}$ is the carrying capacity.

As an example, if $x_{m a x} = 10^{6}$ and $k = 0.5$ as shown above, we cna use Euler's method using a starting value of $0.5 \cdot 10^{6}$ bacteria and a time step of $Δ t = 0.1 hour$ :

Current time $t$	$Δ x = Δ t \cdot k x_{o} (1 - \frac{x}{x_{m a x}})$	New Population $x$
0	$Δ x = 0.1 \cdot (0.5 \cdot 0.5 \cdot 10^{6}) \cdot (1 - \frac{0.5 \cdot 10^{6}}{10^{6}}) = 1.25 \cdot 10^{4}$	5,012,500
0.1	$Δ x = . . .$	...

As such, these models show that the population usually carries towards $x_{m a x}$ over $t \to \infty$ .

Predator-Prey Systems

Usually populations are in competition for resources with each other though. Consider a field and woods shared by rabbits and foxes.

The rabbit population $x$ is governed by the same growth model as the bacteria:

\frac{d x}{d t} = a x (1 - \frac{x}{e}) - b x y

Here:

$a$ : growth rate of rabbits
$e$ : rabbit carrying capacity
$y$ : fox population
$b$ : predation rate

Here we are modelling how the foxes will predate on the rabbits enough to reduce its population. The fox population can only grow while there are rabbits so then it uses:

\frac{d y}{d t} = c b x y - d y

here:

$c$ : growth rate of foxes
$d$ : general "all causes" death rate of foxes

A system of equations helps solve this, and gives the following cyclic results:

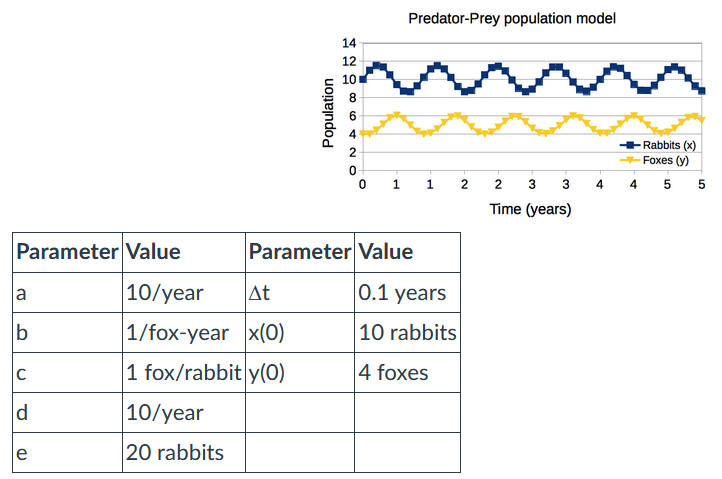
Pasted image 20240429204846.png

Notice the cyclic cyle:

The rabbits overpopulate
This allows more foxes to prey on them, so their size increases while the rabbits decrease
At some point the foxes start starving
With less foxes, the rabbits can overpopulate
(rinse and repeat)

Steady State

These populations will never settle down at any steady state, but they oscillate around this point. By using our equations from above, that's when $x^{'}, y^{'} = 0$ :

\frac{d x}{d t} = a x (1 - \frac{x}{e}) - b x y = 0

\frac{d y}{d t} = c b x y - d y = 0

Solving for our constants, we have the following steady states:

\begin{aligned} (x, y) & = (0, 0) & No population \\ (x, y) & = (e, 0) & Only rabbits \\ (x, y) & = (\frac{d}{b c}, (\frac{a}{b}) (1 - \frac{d}{b c e})) \end{aligned}

Notice that the first two solutions are stable, while the second one is unstable, where solutions near this point move "away" from it.

Carrying Capacity

The factors of $a, b, c, d, . . .$ are all controlled by technology. If a new method of agriculture is made, then we expect to see say $e$ increase as a result. As a result, the carrying capacity has increased as time has moved. The use of tools allows us humans to be able to increase our own numbers in a myriad of ways.

For us, our approximate current carrying capacity is ~9-10 billion humans, where we are at ~7.9 billion. Hence, we will either hit our carrying capacity soon, or we will make new technology that will increase that capacity.

Tipping Points

(continue from canvas)